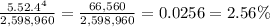Question

In the card game of poker, five cards that have consecutive kinds is called a straight.

An ace can be considered either the lowest card of an A-2-3-4-5 straight or the highest card of a 10-

J-Q-K-A straight. What is the probability that a five-card poker hand contains a straight? For this

problem, you may consider a suited straight (all cards of the same suit) as a straight although the rules

of poker exclude that as a straight.

Answer 1

0.0256 or 2.56 %

Explanation:

There are C(52,5) ways of selecting 5 cards from a deck of 52, where C(52,5) is combinations of 52 taken 5 at a time.

`C(52,5)=\binom{52}{5}= (52!)/(5!(52-5)!)=(52!)/(5!47!)=(52.51.50.49.48)/(5.4.3.2)=2,598,960`

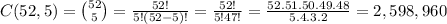
There are 52 ways of choosing a random card. Once that card is chosen, it could be the 1st, 2nd ,3rd ,4th or 5th in the straight.

For each of this possibilities,since poker cards have 4 different kinds, by the rule of product, there are

`52*4^4` possibles straights, so there are
`5*52*4^4` ways of having a straight. The probability of a 5-card straight is

`(5.52.4^4)/(2,598,960)=(66,560)/(2,598,960)=0.0256=2.56\%`