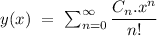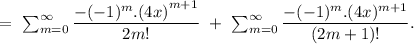Answer:
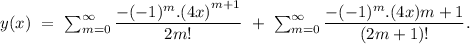
Explanation:
Given differential equation is
We have to find the power series solution of given differential equation about the ordinary point x = 0.
Power series solution of any given differential equation can be given by

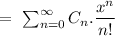

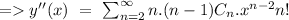
Now, by putting these values in equation (1), we have
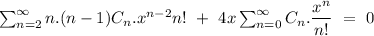
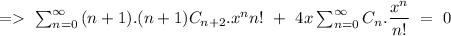
![=>\ \sum_(n=0)^(\infty)[(n+1).(n+2)C_(n+2)+4xC_n]x^n\ =\ 0](https://img.qammunity.org/2020/formulas/mathematics/college/va4vbdfxcxfp3so7myiujrhgjkihvffkfo.png)
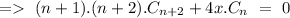

for n = 0

for n = 1
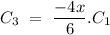
for n = 2
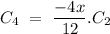
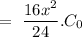
for n = 3
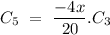
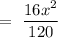
for n=4
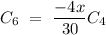
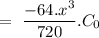
As we can see for
for even value of n i.e n = 2m where m is any integer.
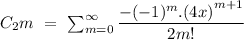
for odd value of n i.e n =2m+1 , where m is any integer.
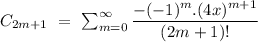
So, the power series solution about the ordinary point x=0, can be given by