Question

A river flows due east at 1.60 m/s. A boat crosses the river from the south shore to the north shore by maintaining a constant velocity of 10.3 m/s due north relative to the water.

a) What is the velocity of the boat relative to shore?
b) If the river is 300 m wide, how far downstream has the boat moved by the time it reaches the north shore?

Answer 1

The velocity of the boat relative to the shore is approximately 10.37 m/s. The boat has moved a distance of approximately 300 meters downstream by the time it reaches the north shore.

Step-by-step explanation:

To find the velocity of the boat relative to the shore, we need to consider the vectors of the river flow and the boat's velocity. Since the boat is moving due north relative to the water, and the river is flowing due east, the two velocities are perpendicular to each other. We can use the Pythagorean theorem to find the total velocity relative to the shore:

Vshore = sqrt[(Vboat)2 + (Vriver)2]

Plugging in the values:

Vshore = sqrt[(10.3 m/s)2 + (1.60 m/s)2]

Vshore ≈ 10.37 m/s

To find how far downstream the boat has moved by the time it reaches the north shore, we can use the formula:

Distance = Vriver * Time

Plugging in the values:

Distance = (1.60 m/s) * Time

The time is equal to the distance divided by the velocity due north:

Time = Distance / Vboat

Plugging in the values:

Time = (300 m) / (10.3 m/s)

Time ≈ 29.13 s

Answer 2

part (a)
`v\ =\ 10.42\ at\ 81.17^o` towards north east direction.

part (b) s = 46.60 m

Step-by-step explanation:

Given,

• velocity of the river due to east =
  `v_r\ =\ 1.60\ m/s.`
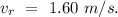
• velocity of the boat due to the north =
  `v_b\ =\ 10.3\ m/s.`

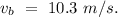
part (a)

River is flowing due to east and the boat is moving in the north, therefore both the velocities are perpendicular to each other and,

Hence the resultant velocity i,e, the velocity of the boat relative to the shore is in the North east direction. velocities are the vector quantities, Hence the resultant velocity is the vector addition of these two velocities and the angle between both the velocities are
`90^o`

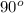
Let 'v' be the velocity of the boat relative to the shore.

`\therefore v\ =\ √(v_r^2\ +\ v_b^2)\\\Rightarrow v\ =\ √(1.60^2\ +\ 10.3^2)\\\Rightarrow v\ =\ 10.42\ m/s.`

Let
`\theta` be the angle of the velocity of the boat relative to the shore with the horizontal axis.

Direction of the velocity of the boat relative to the shore.
`\therefore Tan\theta\ =\ (v_b)/(v_r)\\\Rightarrow Tan\theta\ =\ (10.3)/(1.60)\\\Rightarrow \theta\ =\ Tan^(-1)\left ((10.3)/(1.60)\ \right )\\\Rightarrow \theta\ =\ 81.17^o`

part (b)

• Width of the shore = w = 300m

total distance traveled in the north direction by the boat is equal to the product of the velocity of the boat in north direction and total time taken

Let 't' be the total time taken by the boat to cross the width of the river.
`\therefore w\ =\ v_bt\\\Rightarrow t\ =\ (w)/(v_b)\\\Rightarrow t\ =\ (300)/(10.3)\\\Rightarrow t\ =\ 29.12 s`

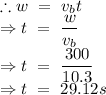
Therefore the total distance traveled in the direction of downstream by the boat is equal to the product of the total time taken and the velocity of the river
`\therefore s\ =\ u_rt\\\Rightarrow s\ =\ 1.60* 29.12\\\Rightarrow s\ =\ 46.60\ m`