Answer:
A = $769.83
Explanation:
Given data:
Principle = $16,500
rate of interest = 3.6%
Number of year = 6 year
period quarterly
Payment to be amortized can be determined by using following relation
![A = P[(r(1+r)^n)/((1+r)^n -1)]](https://img.qammunity.org/2020/formulas/mathematics/college/ruxztw176w27n035vtopp766we4itov35k.png)
r is rate of interest per period is 3.6%\4 = 0.009
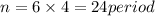
![A = 16500[(0.009(1+0.009)^(24))/((1+0.009)^(24) -1)]](https://img.qammunity.org/2020/formulas/mathematics/college/lyze09yjwf4qwp1iebrv7yromu3oz5z3s9.png)
![A =16500[(0.01159134)/(0.239903796)]](https://img.qammunity.org/2020/formulas/mathematics/college/6b6k6pexoy5tzso5n5or3lz3ridy51rnon.png)
A = $769.83