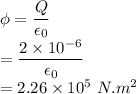Question

A charge q = 2 μC is placed at the origin in a region where there is already a uniform electric field = (100 N/C) . Calculate the flux of the net electric field through a Gaussian sphere of radius R = 10 cm centered at the origin.

a) 2.26 × 105 N · m2/C
b) 5.52 × 105 N · m2/C
c) 1.13 × 105 N · m2/C
d) zero

Answer 1

a)
`2.26*10^5\ N.m^2\C`

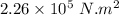
Step-by-step explanation:

Given:

• Magnitude of the point charge ,
  `Q=2\ \rm\mu C`
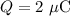
• Strength of the Electric Field E=100 N/C
• Radius of the Gaussian sphere R=10 cm

The net flux due to the uniform Electric E present in the space due to the Gaussian surface will be zero As the the flux which will enter the Gaussian surface will exit the Gaussian surface.

The Electric flux due to the charge placed at the origin is

`\phi =(Q)/(\epsilon_0)\\\pji=(2*10^(-6))/(\epsilon_0)\\\pji=2.26* 10^(5)\ N.m^2\C`