Answer:
(a): Linear charge density of the circular arc =

(b): Surface charge density of the circular arc =
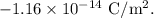
(c): Volume charge density of the sphere =

Step-by-step explanation:
Part (a):
Given:
- Total charge on the circular arc,
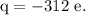
- Radius of the circular arc,

- Angle subtended by the circular arc,
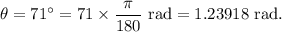
We know, e is the elementary charge whose value is
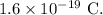
Therefore,
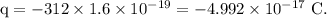
Also, the length l of a circular arc is given as:
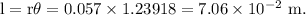
The linear charge density
 of the arc is defined as the charge per unit length of the arc.
of the arc is defined as the charge per unit length of the arc.
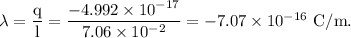
Part (b):
Given:
- Total charge on the circular disc,
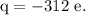
- Radius of the circular disc,
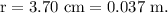
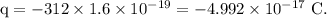
Surface area of the circular disc,
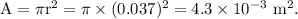
The surface charge density
 of the disc is defined as the charge per unit area of the disc.
of the disc is defined as the charge per unit area of the disc.
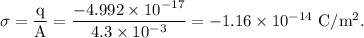
Part (c):
Given:
- Total charge on the sphere,
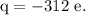
- Radius of the sphere,

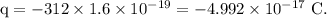
Volume of the sphere,
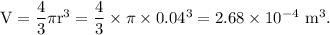
The volume charge density
 of the sphere is defined as the charge per unit volume of the sphere.
of the sphere is defined as the charge per unit volume of the sphere.
