Question

(a) Find all points where the function f(z) = (x^2+y^2-2y)+i(2x-2xy) is differentiable, and compute the derivative at those points.

Answer 1

f is not complex-differentiable

Explanation:

Let the functions u, v defined as follow

`u(x,y)=x^2+y^2-2y`

`v(x,y)=2x-2xy`

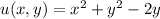
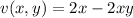
then f can be rewritten as

`f(x,y)=u(x,y)+iv(x,y)`

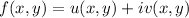
In order for f to be complex-differentiable in a point z=x+iy, it must satisfy the Cauchy-Riemann equations

`(\partial u)/(\partial x)=(\partial v)/(\partial y)`

`(\partial u)/(\partial y)=-(\partial v)/(\partial x)`

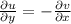
But

`(\partial u)/(\partial x)=2x`

`(\partial v)/(\partial y)=-2x`

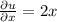
and

`(\partial u)/(\partial x)\\eq (\partial v)/(\partial y)`

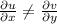
As f does not satisfy the Cauchy-Riemann equations, f is not complex-differentiable.