Question

Consider a colony of E.Coli bacteria that is growing exponentially. A microbiologist finds that, initially, 1,000 bacteria are present and 50 minutes later there are 10,000 bacteria. a) Find expression for the number of bacteria Q(t) after t minutes. b) When will there be 1,000,000 bacteria?

Answer 1

a)
`Q(t)=Q_(0)e^((ln10/50)t)`

b) 150min

Explanation:

a) Using the formula for colony growth
`Q(t)=Q_(0)e^(kt)` we need to find the specific value of k, to do this you'll use the time, initial and final number of colonies provided in your problem.

`Q(t)=Q_(0)e^(kt)\\\\10000=1000e^(k(50)) \\\\(10000)/(1000)=e^(50k) \\\\10=e^(50k)\\ ln(10=e^(50k))\\\\ln10=50k\\\\k=ln10/50\\\\Q(t)=Q_(0)e^((ln10/50)t)\\\\`

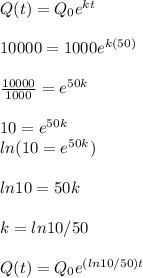
b) Once we have our expression we only have to use our final and initial number of bacteria to find t.

`Q(t)=Q_(0)e^((ln10/50)t)\\\\\\1000000=1000e^(0.046t)\\ 1000=e^(0.046t)\\ln( 1000=e^(0.046t))\\ln1000=0.046t\\t=ln1000/0.046\\t=150 minutes`

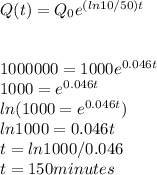
I hope you find this information useful! good luck!