Answer:
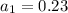 and
and
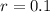 .
.
Explanation:
It is given that Repeated decimals can be written as an infinite geometric series to help convert them to a fraction.
Consider the repeating decimal below.
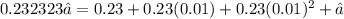
We need to find the value of
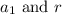 .
.
 is the first term of the series. So,
is the first term of the series. So,
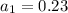
 is the common ratio of the series. So,
is the common ratio of the series. So,
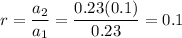
Therefore,
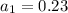 and
and
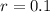 .
.