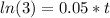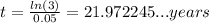Question

Type the correct answer in the box. Round your answer to the hundredth.

An investment in a savings account grows to three times the initial value after tyears.
If the rate of interest is 5%, compounded continuously, t =
I
y ears.

Answer 1

21 YEARS IS CORRECT

Explanation:

Answer 2

Approximately 22.97 years

Explanation:

Use the equation for continuously compounded interest, which uses the exponential base "e":

`A=P e^(k*t)`

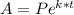
Where P is the principal (initial amount of the deposit - unknown in our case)

A is the accrued value (value accumulated after interest is compounded), in our case it is not a given value but we know that it triples the original deposit (principal) so we write it as: 3 P (three times the principal)

k is the interest rate : 5% which translates into 0.05

and t is the time in the savings account to triple its value (what we need to find)

The formula becomes:

`3P = P e^(0.05 * t)`

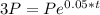
To solve for "t" we divide both sides of the equation by P (notice it cancels P everywhere), and then to solve for the exponent "t" we use the natural logarithm function:

`(3P)/(P) = (P)/(P)  e^(0.05 * t)`

`3 = e^(0.05 * t)`

`ln(3) = 0.05 * t`

`t = (ln(3))/(0.05) = 21.972245... years`