Question

A baseball diamond is a square whose sides are 9090 feet long. Suppose a player running from second base to third base has a speed of 30 feet per second at the instant he is 20 feet from third base. At what rate is the player’s distance from home plate changing at that instant?

Answer 1

Rate of change of distance at that instant = 0.066 ft/sec

Explanation:

In the question,

The baseball field is in the square diamond shape.

Side length of square = 9090 ft.

Now,

The player runs from the 2nd base to the 3rd base.

Speed of running of player, v = 30 ft/ sec.

Distance of the player from third base = 20 ft.

Now,

Let us say the distance of the player from the Home base is = l

So,

In the triangle using the Pythagoras theorem, we get,

`l^(2)=x^(2)+s^(2)`

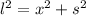
where, 'x' is the distance of the player from the third base and 's' is the side of the square field base.

So,

`l^(2)=x^(2)+s^(2)\\On\,differentiating\,we\,get,\\2l(dl)/(dt)=2x(dx)/(dt)\\l(dl)/(dt)=x(dx)/(dt)\\`

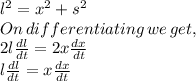
Now,

Also, at the moment when, x = 20,

Length from the Home base is,

`l^(2)=20^(2)+9090^(2)\\l=9090.022\,ft.`

Now,

On putting we get,

`l(dl)/(dt)=x(dx)/(dt)\\(9090.022)(dl)/(dt)=20(30)\\(dl)/(dt)=0.066\,ft./sec.`

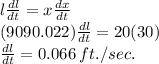
Therefore, the rate of change of distance from the home plate is 0.066 ft/s