Question

Which of the following quadratic functions has a graph that opens downward? Check all that apply.

A. Y=60x-15x^2
B. Y= -(5+2x^2)
C. 2x^2-9x+3
D. X^2+4x+8

Answer 1

A & B

Explanation:

A&B are your answers since they're the only ones which has negative in their equations for the
`x^(2)` term.

Whereas C is a linear equation and D opens upward since
`x^(2)` is positive.

Hope this helps!

Answer 2

A.
`y=60x-15x^2`

B.
`y= -(5+2x^2)`

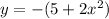
Explanation:

Since, a quadratic function with the negative leading coefficient is always opens downward,

Note :

Leading coefficient : the coefficient (constant value written before a variable) which variable has the highest exponent.

In quadratic function the coefficient before the variable with exponent 2 is leading coefficient,

In
`y=60x-15x^2`

Leading coefficient = -15 ( negative )

⇒ it opens downward,

In
`y=-(5+2x^2)`

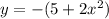
Leading coefficient = -2 ( negative )

⇒ it opens downward,

In
`y=2x^2-9x+3`

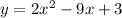
Leading coefficient = 2 ( positive )

⇒ it does not open downward,

In
`y=x^2+4x+8`

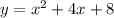
Leading coefficient = 1 ( positive )

⇒ it does not open downward.