Question

The captain of a plane wishes to proceed due west. The cruising speed of the plane is 256 m/s relative to the air. A weather report indicates that a 44.3-m/s wind is blowing from the south to the north. In what direction, measured with respect to due west, should the pilot head the plane?

Answer 1

Angle = 9.965° South of West.

Step-by-step explanation:

In the question,

The speed of the Plane w.r.t to Wind = 256 m/s

Speed of the Wind w.r.t to Ground = 44.3 m/s

Direction of Wind = North from South

Direction Plane wishes to go = West

So,

Using the vectors,

Speed of Wind w.r.t Ground is given by,

`v_(w,g)=44.3j`

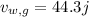
Resultant speed of Plane w.r.t Ground is given by,

`v_(p,g)=-A(i)`

So,

From the Vector's Triangle Sum property,

`v_(p,w)=v_(p,g)-v_(w,g)\\v_(p,w)=-Ai-44.3j`

Therefore, the plane has to move in the direction of 'III quadrant' or 'South-West' direction.

Now,

In the triangle, using Pythagoras Theorem,

`(256)^(2)=(44.3)^(2)+(v_(p,g))^(2)\\v_(p,g)=√(63573.51)\\v_(p,g)=252.13\,m/s`

The speed of the plane = 252.13 m/s

Now,

`sin\theta=(v_(w,g))/(v_(p,w))=(44.3)/(256)=0.173\\\theta=sin^(-1)(0.173)\\\theta=9.965`

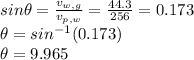
Therefore, the angle at which the plane should fly to go West is = 9.965° South of West.