Answer:
a) The magnitud will be
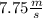 .
.
b) The direction of the ball's velocity relative to Juan will be
 .
.
Step-by-step explanation:
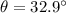
Juan's velocity relative to the ground :
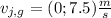
Ball's velocity relative to the ground :
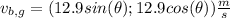
We know that Ball's velocity relative to the ground is Ball's velocity relative to Juan plus Juan's velocity relative to the ground. This is a very important notion that even extends to more complex mathematical problems (differentiation).
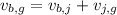 ⇒
⇒
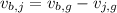
⇒
(m)/(s) - (0 ; 7.5)(m)/(s)](https://img.qammunity.org/2020/formulas/physics/high-school/wu5zycfgvmebgvgnb2svkosj7zzwhy4aba.png) [/tex]
[/tex]
∴
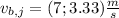
a) The magnitud will be
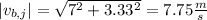 .
.
b) The direction of the ball's velocity relative to Juan will be:
 ⇒
⇒
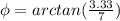
∴
 .
.