Answer:
The spaceship will take 850.34 hours to reach a speed of 0.1c and it will travel 45 918 367 346.9 km before reaching that speed.
Step-by-step explanation:
The spaceship is traveling at a constant acceleration, then we can use the kinematic equations for that kind of movement to calculate the time it would take to reach a given speed.
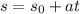
Where
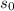 is the initial speed,
is the initial speed,
 is the acceleration rate and
is the acceleration rate and
 is the speed the spaceship will have at a time
is the speed the spaceship will have at a time
 .
.
If the spaceship starts from a stop, then
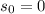 . So:
. So:
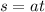

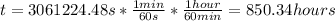
Then, the spaceship will take 850.34 hours to reach a speed of 0.1c
To calculate the displacement of the spaceship during that time, we use the following equation:
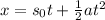
Where
 is again the initial speed (which is zero),
is again the initial speed (which is zero),
 is the acceleration and
is the acceleration and
 is the travel time (which we've calculated is the previous step).
is the travel time (which we've calculated is the previous step).
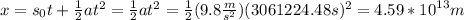
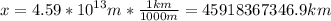
Then, the spaceship will travel 45 918 367 346.9 km before reaching a 0.1c speed.