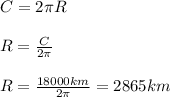Question

An extraterrestrial "Eratosthenes" performs the equivalent experiment, that Eratosthenes did on Earth, on her/his home world. She/He measures the angle of the shadow in her/his alien hometown (Alexandria) to be 10 degrees and the distance to the alien well (Syene) to be 500 km. What is the radius that the alien Eratosthenes estimates for her/his planet?

a. 2865 km
b. 9065 km
c. 18024 km
d. 1500 km
e. 31415 km

Answer 1

a. 2865 km

Step-by-step explanation:

Eratosthenes observed that the sun's rays formed a vertical angle of 7º 12 ’. Which confirmed that the Earth was not flat, assuming that it had a spherical shape, using the distance between Alexandria and Siena and the measure of the angle of inclination of the solar rays in Alexandria, calculated the circumference of the Earth.

The calculation was made with a simple rule of three:

angle of inclination of the solar rays——————- distance

360º ————- Planet circumference

`C=(distance*360^\circ)/(angle)\\\\C=(500km*360^\circ)/(10^\circ)=18000km`

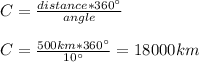
And since we know that:

`C=2\pi R\\\\R=(C)/(2\pi)\\\\R=(18000km)/(2\pi)=2865km`