Answer:
(4). 8/3 ft/sec.
Speed of person's shadow growing = 2.66 ft/sec.
Step-by-step explanation:
In the question,
The height of the pole is = 15 foot
Height of the person = 6 foot
Rate of walking away from the pole, v = dy/dt = 4 ft/sec.
Now,
Let us say the length of shadow is = x
and,
Distance of person from the pole is = y
So,
In the triangle EDC and EAB, from the similar triangle properties, we can say,
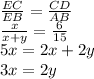
Now,
On differentiating the equation w.r.t, time, t, we get,
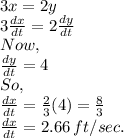
Therefore, the Speed at which the person's shadow is growing is 2.66 ft/sec.
Hence, the correct option is (4).