Question

An object is dropped from 22 feet below the tip of the pinnacle atop a 1178​-ft tall building. The height h of the object after t seconds is given by the equation h equals negative 16 t squared plus 1156. Find how many seconds pass before the object reaches the ground.

Answer 1

t = 8.5 sec

Step-by-step explanation:

Given,

• Height of the tower = H = 1178 ft
• Height of the release point of the object = 22 ft

Let 't' be the time taken by the object to reach the ground.

At the ground height = h = 0

From the expression of the height of the object in time 't' is

`h\ =\ -16t^2\ +\ 1156`

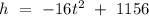
At the ground height of the ball is 0 m and the time taken is t

From the substitution of these values in the above equation, we get,

`\therefore 0\ =\ -16t^2\ +\ 1156\\\Rightarrow 16t^2\ = \ 1156\\\Rightarrow t\ =\ \sqrt{(1156)/(16)}\\\Rightarrow t\ =\ 8.55 sec.`

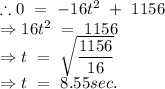
Hence, the required time taken by the ball to reach at the ground is 8.55 sec.