Question

Two particles of identical massmare acted on only by the gravitational force of one upon the other. If the distance d between the particles is constant, what is the angular velocity of the line joining them? Use Newton’s second law with the center of mass of the system as the origin of the inertial frame

Answer 1

The angula velocity is given by:

`w=\sqrt{(2Gm)/(d^3) }`.

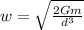Step-by-step explanation:

Newton's law of universal gravitation tells us that the force acting between any to masses is:

`{\displaystyle F=G{\frac {m_(1)m_(2)}{d^(2)}},}`

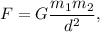
Where d is the distance between the masses and G is the gravitational constant.

If
`m_1=m_2=m`,

`{\displaystyle F=G{\frac {m^2}{d^(2)}},}`

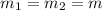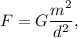
By Newton’s second law, we now that in magnitud the force acting on
`m_1` (
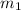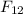`F_(12)`) is equal to the force acting on
`m_2` (
`F_(21)`):

`F=F_(12)=F_(21)=G{\frac {m^2}{d^(2)}},}`

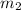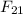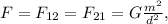
Also we know that angular velocity
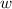`w` relates to centripetal acceleration by:
`a_c=rw^2`.

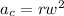At the same time we know that:
`ma_c=F=G{\frac {m^2}{d^(2)}},}`

⇒
`a_c=G{\frac {m}{d^(2)}}}`

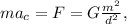
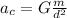
Now:
`w=\sqrt{(a_c)/(r) } = \sqrt{(Gm)/(r^2d) }`

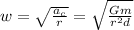
Considering that d=2r, we finally have:

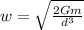`w=\sqrt{(2Gm)/(d^3) }`.