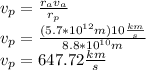Question

The orbit of Halley's Comet around the Sun is a long thin ellipse. At its aphelion (point farthest from the Sun), the comet is 5.700 × 1012 m from the Sun and moves with a speed of 10.00 km/s. What is the comet's speed at its perihelion (closest approach to the Sun) where its distance from the Sun is 8.800 × 1010 m? The mass of the Sun is 1.987 × 1030 kg.

Answer 1

`v_(p)=647.72(km)/(s)`

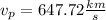
Step-by-step explanation:

According to Kepler's second law: a line segment joining an object and the Sun sweeps out equal areas during equal intervals of time. This law is equivalent to the constancy of the angular momentum, that is to say:

`\Delta \vec{L}=0\\\vec{L}_(p)=\vec{L}_(a)\\m*(\vec{r}_(p)* \vec{v}_(p))=m*(\vec{r}_(a)* \vec{v}_(a))\\mr_(p) v_(p)sin (\theta)=mr_(a) v_(a)sin (\theta)`

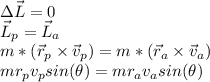
Here,
`m` is the comet's mass,
`r` is its distance from the Sun,
`v` is its speed and
`\theta` the angle between
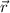`\vec{r}` and
`\vec{v}`

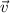
The aphelion and the perihelion are the only two points in the orbit where the radius and velocity are perpendicular. Therefore, at these 2 points, the angular momentum module can be calculated as a simple product:

`mr_(p) v_(p)sin (^\circ 90)=mr_(a) v_(a)sin (^\circ 90)\\mr_(p) v_(p)=mr_(a) v_(a)`

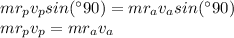
Rewriting for
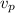`v_(p)`:

`v_(p)=(r_(a)v_(a))/(r_(p))\\v_(p)=((5.7*10^(12)m)10(km)/(s))/(8.8*10^(10)m)\\v_(p)=647.72(km)/(s)`