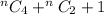Answer:
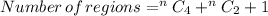
Explanation:
In the question,
There are 'n' points on the circle.
For making the maximum number of regions we can do that by selecting 2 points from the given number of points.
i.e.
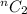
And,
By selecting 4 points from the given number of points we get the extra regions formed on the intersection of the chords with each other.
i.e.
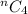
And, 1 more region.
So, we can write it as,
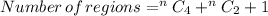
Therefore, the number of regions formed from the 'N' points are,