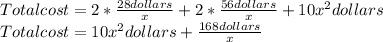Question

A rectangular storage container with an open top has a volume of 14 m3. The length of its base is twice its width. Material for the base costs $5 per square meter; material for the sides costs $4 per square meter. Express the cost of materials as a function of the width of the base.

Answer 1

`Total cost=10x^(2) dollars+(168dollars)/(x)`

Step-by-step explanation:

First at all, let's see the figure in the attachment where we define:

Width is "x", Lenght must be "2x" and Height is "h".

The volume of a rectangular storage container is defined as:

V=lengh*width*height

So, replacing values, we have:

V=
`2x^(2) h`

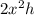
Considering that V=14m3 we can clear "h" in function of "x" (the width):

`V=2x^(2) h=14; h=(7)/(x^(2))`

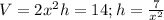
Now, we calculate the areas of the container:

`Ax_(1) =x*h\\Ax_(2)=2x*h\\Ax_(3)=2x*x`

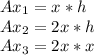
Where: Ax1 is the side 1 area; Ax2 is the side 2 area and Ax3 is the base area

Replacing "h" on the previous equations, we have:

`Ax_(1)=x*h=x*(7)/(x^(2) )=(7)/(x)\\Ax_(2)=2x*h=2x*(7)/(x^(2) )=(14)/(x)\\Ax_(3)=x*2x=2x^(2)`

Remember that the container is open at the top, so we have to calculate just one area in the base. The sides 1 and 2 are 2 of each one.

So, we have: Total area = 2*Ax1 + 2*Ax2 + Ax3

Now for the total cost of materials, we have: Total cost=Cost (2*Ax1) + Cost (2*Ax2) + Cost (Ax3)

For the sides 1 and 2, we have a cost of:

`Cost Ax_(1)=(7)/(x)m^(2) *(4 dollars)/(m^(2) )=(28dollars)/(x)\\Cost Ax_(2)=(14)/(x)m^(2) *(4 dollars)/(m^(2) )=(56dollars)/(x)\\Cost Ax_(3)=(2x^(2))m^(2)*(5 dollars)/(m^(2))=10x^(2)dollars\\`

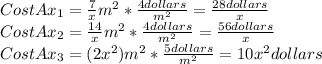
Finally, total cost is:

`Total cost=2*(28 dollars)/(x) + 2*(56 dollars)/(x) + 10x^(2) dollars\\Total cost=10x^(2) dollars+(168dollars)/(x)`