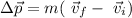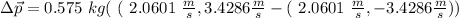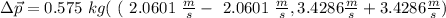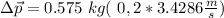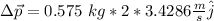Answer:
Taking the x axis to the right and the y axis to be up, the total change of momentum is

Step-by-step explanation:
The momentum
 is given by:
is given by:
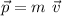
where m is the mass and
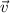 is the velocity. Now, taking the suffix i for the initial condition, and the suffix f for the final condition, the change in momentum will be:
is the velocity. Now, taking the suffix i for the initial condition, and the suffix f for the final condition, the change in momentum will be:
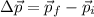
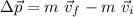
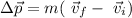
As we know the mass of the ball, we just need to find the initial and final velocity.
Knowing the magnitude and direction of a vector, we can obtain the Cartesian components with the formula
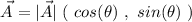
where
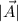 is the magnitude of the vector and θ is the angle measured from the x axis.
is the magnitude of the vector and θ is the angle measured from the x axis.
Taking the x axis to the right and the y axis to be up, the initial velocity will be:
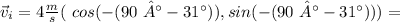
where minus sign appears cause the ball is going downward, and we subtracted the 31 ° as it was measured from the y axis
So, the initial velocity is
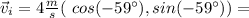

The final velocity is
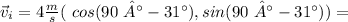

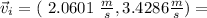
So, the change in momentum will be