Question

10) Let λ 0.60 i .80 j and . 1 → = ˆ + 0 ˆ λ 0.50 i .866 j 2 → = ˆ + 0 ˆ 1. Show that both the vectors are unit vectors. 2. Is the sum of these two unit vectors also a unit vector? If not, find a unit vector along the sum of λ and . 1 → λ2

Answer 1

2.
`0.55099\ \hat i+0.8345\ \hat j.`

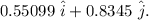
Explanation:

Given vectors are:

• 
  `\vec \lambda_1=0.60\ \hat i+0.80\ \hat j.`
• 
  `\vec \lambda_2 = 0.50\ \hat i+0.866\ \hat j.`

where,
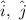`\hat i,\ \hat j` are the unit vectors along positive x and y axes respectively.

(1):

A vector is called unit vector if its magnitude (length) is 1 and the magnitude of a vector
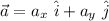`\vec a = a_x\ \hat i+a_y\ \hat j` is given by

`a=√(a_x^2+a_y^2).`

Therefore,

The magnitude of
`\vec \lambda_1` =
`√(0.60^2+0.80^2)=1.00.`

The magnitude of
`\vec \lambda_2` =
`√(0.50^2+0.866^2)=0.999978\approx 1.00.`

Thus, both the vectors are unit vectors.

(2):

The sum of these vectors is given by

`\vec \lambda_1+\vec \lambda_2=(0.60\hat i+0.80\hat j)+(0.50\hat i+0.866\hat j)\\=(0.60+0.50)\hat i+(0.80+0.866)\hat j\\=1.10\ \hat j+1.666\ \hat j.`

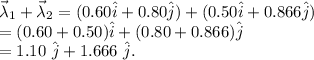
The magnitude of the sum of these vectors =
`√(1.10^2+1.666^2)=1.9964.`

Thus, it is not a unit vector.

The unit vector along the direction of sum of these two vectors is given by

`\hat \lambda =(\vec \lambda_1+\vec \lambda_2)/(|\vec \lambda_1+\vec \lambda_2|)=(1.10\ \hat j+1.666\ \hat j)/(1.9964)=0.55099\ \hat i+0.8345\ \hat j.`