Answer: 0.0454 N
Step-by-step explanation:
Weight
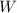 is defined as the force with which a planet (or moon, or massive body) attracts a body or object by the action of gravity force. Mathematically is expressed as:
is defined as the force with which a planet (or moon, or massive body) attracts a body or object by the action of gravity force. Mathematically is expressed as:
 (1)
(1)
Where:
 is the mass of the object
is the mass of the object
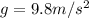 on Earth
on Earth
Now, in this problem we are asked to find the weight of a spherical rock found in Titan, but measured on Earth. This means we have to use
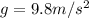 .
.
On the other hand, we know the density of this rock is
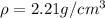 and its volume is
and its volume is
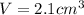 .
.
If density is expressed as:
 (2)
(2)
We can find the mass of the rock from this equation:
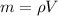 (3)
(3)
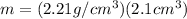 (4)
(4)
 (5) This is the mass of the rock in kilograms
(5) This is the mass of the rock in kilograms
So, substituting this mass (5) in (1), we can finally find the weight of the rock measured for Earth:
 (6)
(6)
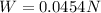 (7)
(7)