Answer:
x=4, y=4, λ=-16
Explanation:
We have this 3x3 system of linear equations:
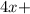 λ
λ
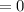
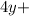 λ
λ
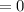
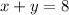
So, let's rewrite the system in its augmented matrix form
![\left[\begin{array}{cccc}4&0&1&0\\0&4&1&0\\1&1&0&8\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/v17tuie8gs4utp9vobcb7tg9vw5gi2fz4e.png)
Let´s apply row reduction process to its associated augmented matrix:
Swap R1 and R3
![\left[\begin{array}{cccc}1&1&0&8\\0&4&1&0\\4&0&1&0\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/eyvpyikn8sq41ecyvyvovv0nwguuel5lt3.png)
R3-4R1
![\left[\begin{array}{cccc}1&1&0&8\\0&4&1&0\\0&-4&1&-32\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/lewce3sjgits49ygj5hbv7qh77dzpkvl14.png)
R3+R2
![\left[\begin{array}{cccc}1&1&0&8\\0&4&1&0\\0&0&2&-32\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/9fmq5574cwwh8btyzdfdyi19csnkvoybv2.png)
Now we have a simplified system:
x+y+0=0
0+4y+λ=0
0+0+2λ=-32
Solving for λ, x, and y
λ=-16
x=4
y=4