Answer:
He should plant 100 acres of corn and 400 acres of wheat.
Explanation:
This problem can be solved by a siple system of equations.
]x denotes the number of acres of corn
y denotes the number of acres of wheat
Building the system:
The Johnson Farm has 500 acres of land allotted for cultivating corn and wheat. This means that:
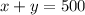
The cost of cultivating corn and wheat (including seeds and labor) is $42 and $30 per acre, respectively. Jacob Johnson has $16,200 available for cultivating these crops. This means that:
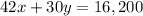
So, we have the following system
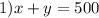
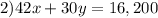
If he wishes to use all the allotted land and his entire budget for cultivating these two crops, how many acres of each crop should he plant?
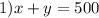
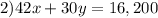
I am going to write y as a function of x in 1), and replace in 2). So:
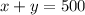 means that
means that
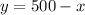
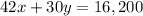
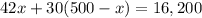
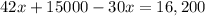
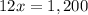
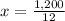
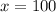
Now, going back to 1:
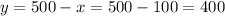
He should plant 100 acres of corn and 400 acres of wheat.