Question

A state administered standardized reading exam is given to eighth grade students. The scores on this exam for all students statewide have a normal distribution with a mean of 507 and a standard deviation of 39. A local Junior High principal has decided to give an award to any student who scores in the top 10% of statewide scores. How high should a student score be to win this award? Give your answer to the nearest integer. For help on how to input a numeric answer, please see the instructions for entering numeric response.

Answer 1

The minimum score to be obtained to place in the top 10% and win this award is, 557

Explanation:

Since the score obtained by eighth grade students is a normal random variable with a mean
`\mu = 507` and
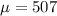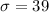`\sigma= 39` and we are interested in the minimum score required for a student to be in the top 10% of all scores, It is necessary to calculate the 90th percentile for the cumulative probability distribution of the score variable in the reading test.

The variable
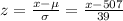`z =(x-\mu)/(\sigma)=(x-507)/(39)` is a standard normal variable and therefore,
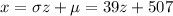`x = \sigma z+\mu=39z+507` is the score corresponding to the standardized value z.

We must calculate the value of k such that
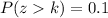`P (z> k) = 0.1`, then, using the inverse standard normal distribution you have to
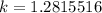`k = 1.2815516` y hence
`x = (39)(1.2815516)+507=556.98051`

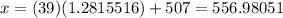
Conclusion: The minimum score to be obtained to place in the top 10% is 557