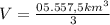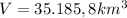Question

I need help with 18 PLEASE!!!!

Answer 1

`V=35.185,8 km^(3)`

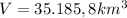
Explanation:

The volume of a cone can be calculated using the following formula:

`V=(\pi . r^(2).h )/(3) \\R= radius\\H=height`

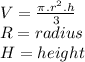
We know that the radius is the half of the figure's diameter. In this excercise:

`r= 80 km : 2 = 40 km`

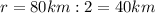
Height in this case is 21 km.

So supplanting we get:

`V=(\pi.(40km)^(2).21km  )/(3)`

`V=(\pi.1600km^(2).21km  )/(3)`

`V=(\pi.1600km^(2).21km  )/(3)`

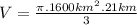
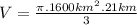
We have in total three "km"'s, and that is equal to
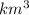`km^(3)`. Remember that when we want to calculate a volume, the unit has to be raised to the third power.

`V=(\105.557,5 km^(3)  )/(3)`

`V=35.185,8 km^(3)`