Question

Suppose that you need to create a list of n values that have a specific known mean. Some of the n values can be freely selected. How many of the n values can be freely assigned before the remaining values are​ determined? (The result is referred to as the number of degrees of​ freedom.)

Answer 1

As the problem indicates, degrees of freedom are the number of values ​​that can be independently selected before it is necessary to choose specific values ​​to arrive at the desired result.

The average, on the other hand, results from the sum of a list of values ​​divided by the amount of values ​​in the summed list.

Assume that the mean sought is
`x` and consider that the list is composed of a single element
`a`, in that case no random number can be selected, since the mean
`x` must correspond to that number.

If the list were composed of two elements
`a` and
`b`, one of the two values ​​could be chosen randomly, and according to the chosen value the second should be the one whose sum with the previous one results in
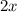`2x`, this given that the formula of the average
`\sum\limits_(i=1)^n ( x_(i))/(n)`.

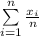With three values ​​
`a`,
`b` and
`c`, it is possible to select two freely, since the thirteen must be the one that balances the sum of
`a+b`, that is
`(a + b) + c = 3x`.

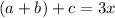Thus, in general, with n values, it is possible to select
`n-1` values ​​freely whose sum must be balanced by the last value so that the whole sum is
`nx`.

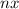Answer

In a list of
`\bf{n}` values ​​you can assign
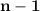`\bf{n-1}` values ​​freely, that is, you have
`n-1`degrees of freedom.