Answer:
0,37
Explanation:
It will be easier if we noun the events.
A= Cindi's friend comes to England.
B= New England is mostly cloudly.
We are searching the probability of just A doesn´t happen or just A happens but not B.
The probability of A doesn´t happen is one minus the probability of A:
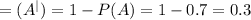
The events A and B are independent for this reason the probability than both occurs is the product of the probability of each event. It means:
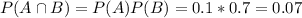
The probability of A doesn´t happen or A and B happen is:
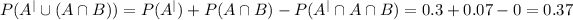
Conclusively we have to rest the probability of A doesn´t happen and A and B happen, but A happens and doesn´t happen and the same time is impossible. For this reason, we have the same result.
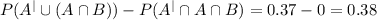
Then the probability either Cindi's friend does not come to New England, or she does come but it is mostly cloudy is 0.37