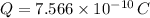Question

A long cylindrical shell (radius = 2.0 cm) has a charge uniformly distributed on its surface. If the magnitude of the electric field at a point 8.0 cm radially outward from the axis of the shell is 85 N/C, how much charge is distributed on a 2.0-m length of the charged cylindrical surface?

Answer 1

`Q= 7.566 * 10 ^(-10) \, C`

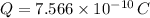
Step-by-step explanation:

Applying Gauss' Law to a cylindrical shell of radius 8 cm and height h, concentric to the charged shell, we get:

`E(r) \cdot 2 \pi r  h= \cfrac{\lambda h}{\epsilon_o}`

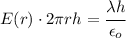
Where
`\lambda` is the charge per unit length, and so
`\lambda h = Q` is the charge inside the shell, and if we set
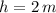`h=2\, m` we can get the answer to our question.

Solving for
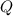`Q` we get:

`Q= \epsilon_o E(r) 2 \pi r h`

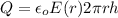
plugging in the values ( in SI units) we get:

`Q= 7.566 * 10 ^(-10) \, C`