Answer:
The entering car is going to catch up with the other car after 20.76 seconds.
Explanation:
The car leaving the pit area is moving with a constant accelaration, then we can calculate the speed it has when entering the main speedway using the following equation:
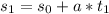
Where
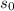 is the initial speed (which is zero given that the car starts froms rest),
is the initial speed (which is zero given that the car starts froms rest),
 is the car's accelaration and
is the car's accelaration and
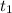 is the time passed until it reaches the main speedway.
is the time passed until it reaches the main speedway.
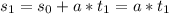

For an object travelling at a constant accelation, the displacement
 at a time
at a time
 can be calculate using the following equation:
can be calculate using the following equation:
 (equation 1)
(equation 1)
Let's consider
 the point where the first car enters the main speedway. If
the point where the first car enters the main speedway. If
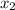 is the point where this car catch up with other one after
is the point where this car catch up with other one after
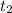 seconds, we may rewrite the equation 1 like this:
seconds, we may rewrite the equation 1 like this:

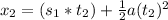 (equation 2)
(equation 2)
In other hand, the second car is travelling at a constant speed
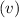 when it meets the entering car. Then, its displacement
when it meets the entering car. Then, its displacement
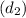 after
after
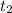 seconds can be calculated using the following formula:
seconds can be calculated using the following formula:
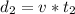 (equation 3)
(equation 3)
The entering car is going to catch up with the other one when
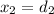 , so when can find how much time this will require equaling equations 2 and 3 and isolating
, so when can find how much time this will require equaling equations 2 and 3 and isolating
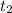
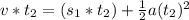
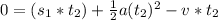
![[(1)/(2)(a*t_2)-(v-s_1)]*t_2=0](https://img.qammunity.org/2020/formulas/mathematics/high-school/5kt9jz1ysy7ifhsp45jwfsocp69zeibckw.png)

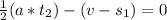
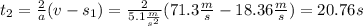
So, the entering car is going to catch up with the other car after 20.76 seconds.