Question

The logistic equation has been used to model the spread of technology. Let N∗ be the number of ranchers in Uruguay, and N(t) the number who have adopted a new pasture technology. The rate of adoption dN/dt is proportional to the number who have adopted the technology, and the fraction who have not (and thus are susceptible to changing). So the equation is dN dt = αN 1 − N N∗ According to a study by Banks (1993), N∗ = 17, 015, N(0) = 141, α = 0.49 per year. Determine how long it takes for the new technology to be adopted by 80% of the population of ranchers.

Answer 1

12.6 years

Explanation:

The equation of adoption of the pastures is

`(dN)/(dt)= a*N*(1-(N)/(N^(*) ) )\\`

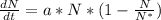
Rearranging we have

`(dN)/(N*(1-(N)/(N^(*)) ))={a*dt}`

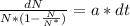
Integrating

`\int(dN)/(N*(1-(N)/(N^(*)) ))=\int{a*dt}\\-ln((N^(*) )/(N)-1)+C=a*t`

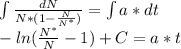
At t=0, N(0)=141

`-ln((N^(*) )/(N)-1)+C=a*t\\-ln(17015/141-1)+C=0.49*0\\C=ln(17015/141-1)=ln(119.67)=4.785\\`

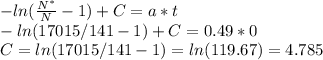
The 80% of the population of ranchers represents 0.8*17015=13612 ranchers, so the time needed to reach that ammount of adoption is

`-ln((N^(*) )/(N)-1)+C=a*t\\\\-ln(17015/13612-1)+4.785=0.49*t\\1,386+4.785=0.49*t\\t= 6.171/0.49 = 12.6`

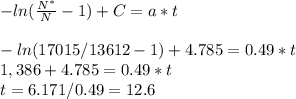
The time it takes for a 80% adoption is 12.6 years