Question

A tank originally contains 160 gal of fresh water. Then water containing 1 4 lb of salt per gallon is poured into the tank at a rate of 4 gal/min, and the mixture is allowed to leave at the same rate. After 8 min the process is stopped, and fresh water is poured into the tank at a rate of 6 gal/min, with the mixture again leaving at the same rate. Find the amount of salt in the tank at the end of an additional 8 min.

Answer 1

After the first 8 minutes, the amount of salt in the tank remains the same. After the next 8 minutes, the amount of salt in the tank is 0 pounds.

Step-by-step explanation:

We start with 160 gallons of fresh water in the tank.

For the first 8 minutes, water containing 1/4 pound of salt per gallon is poured into the tank at a rate of 4 gallons per minute, and the mixture is allowed to leave at the same rate. This means that in 8 minutes, 32 gallons of water containing salt are added to the tank, and the same amount leaves the tank.

After the first 8 minutes, there are 160 + 32 - 32 = 160 gallons of water in the tank, and the amount of salt in the tank remains the same.

Then, fresh water is poured into the tank at a rate of 6 gallons per minute, and the mixture is allowed to leave at the same rate. In the next 8 minutes, 48 gallons of fresh water are added to the tank, and the same amount leaves the tank.

After the next 8 minutes, there are 160 + 48 - 48 = 160 gallons of fresh water in the tank, and the amount of salt in the tank remains 0 pounds.

Therefore, at the end of the additional 8 minutes, the amount of salt in the tank is 0 pounds.

Answer 2

245.86 lb of salt

Step-by-step explanation:

Let y(t) be the amount of salt in the tank at instant t. Then y'(t) represents the rate of change of the amount of salt in the tank at instant t.

The water entering the tank contains 14 lb of salt per gallon and enters at a speed of 4 gal/min, so every minute 14*4=56 lb of salt are entering the tank the first 8 min.

`y'(t)=56\;(0\leq t\leq 8)`

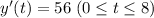
After 8 minutes, as the volume of tank keeps 160 gal., the concentration of salt is
`(y(t))/(160)`.

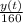Since the water is now leaving the tank at 6 gal/min, the salt is leaving the tank at a speed of
`-6(y(t))/(160)=-0.0375y(t)`.

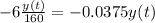Notice that the speed is negative because the salt is leaving the tank, so the amount of salt is decreasing.

Now we have the following ordinary differential equation

`y'(t)=56 \; 0 \leq t \leq 8`

`-0.0375y(t) \; 8 \leq t \leq 16`

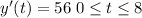
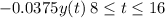
Solving this differential equation we get a piecewise function defined as follow

`y(t) = 56t + C \; (0\leq t\leq 8)`

where C is a constant.

Since the tank had no salt at the beginning of the process. Y(0)=0, so

`y(t) = 56t \; (0\leq t\leq 8)`

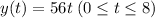
For
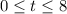`0\leq t\leq 8` we have

`y'(t)=-0.0375y(t)`

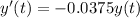
and solving this equation we get

`y(t)=Ce^(-0.0375t)`

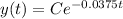
where C is a constant that can be found with the initial condition y(8) = 56*8 = 448

and our solution is

`y(t)=56t \; 0 \leq t \leq 8`

`448e^(-0.0375t) \; 8\leq t\leq 16`

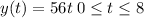
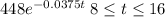
To know what the amount of salt is at the end of the process, we must evaluate y(16), which is

`y(16)=448e^(-0.0375*16)=448*0.5488\approx 245.867`

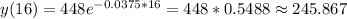
So, at the end of the process the tank contains 245.867 lb of salt.