Question

A cannon fires a 0.2 kg shell with initial velocity vi = 9.2 m/s in the direction θ = 46 ◦ above the horizontal. The shell’s trajectory curves downward because of gravity, so at the time t = 0.555 s the shell is below the straight line by some vertical distance ∆h. Find this distance ∆h in the absence of air resistance. The acceleration of gravity is 9.8 m/s 2 .

Answer 1

∆h = 0.071 m

Step-by-step explanation:

I rename angle (θ) = angle(α)

First we are going to write two important equations to solve this problem :

Vy(t) and y(t)

We start by decomposing the speed in the direction ''y''

`sin(\alpha) = (Vyi)/(Vi)`

`Vyi = Vi.sin(\alpha ) = 9.2 (m)/(s) .sin(46) = 6.62 (m)/(s)`

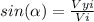
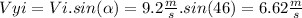
Vy in this problem will follow this equation =

`Vy(t) = Vyi -g.t`

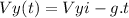
where g is the gravity acceleration

`Vy(t) = Vyi - g.t= 6.62 (m)/(s) - (9.8(m)/(s^(2) )) .t`

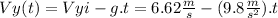
This is equation (1)

For Y(t) :

`Y(t)=Yi+Vyi.t-(g.t^(2) )/(2)`

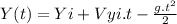
We suppose yi = 0

`Y(t) = Yi +Vyi.t-(g.t^(2) )/(2) = 6.62 (m)/(s) .t- 4.9(m)/(s^(2) ) .t^(2)`

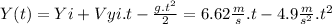
This is equation (2)

We need the time in which Vy = 0 m/s so we use (1)

`Vy (t) = 0\\0=6.62 (m)/(s) - 9.8 (m)/(s^(2) ) .t\\t= 0.675 s`

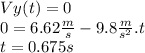
So in t = 0.675 s → Vy = 0. Now we calculate the y in which this happen using (2)

`Y(0.675s) = 6.62(m)/(s).(0.675s)-4.9 (m)/(s^(2) )  .(0.675s)^(2) \\Y(0.675s) =2.236 m`

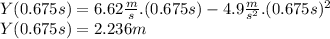
2.236 m is the maximum height from the shell (in which Vy=0 m/s)

Let's calculate now the height for t = 0.555 s

`Y(0.555s)= 6.62 (m)/(s) .(0.555s)-4.9(m)/(s^(2) ) .(0.555s)^(2) \\Y(0.555s) = 2.165m`

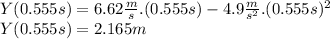
The height asked is

∆h = 2.236 m - 2.165 m = 0.071 m