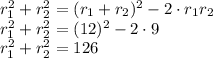Answer:
The value of
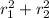 is 126
is 126
Explanation:
We can use the definition of Vieta's formula for quadratics:
Given
 , if the equation f(x) = 0 has roots
, if the equation f(x) = 0 has roots
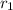 and
and
 then
then
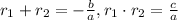
So suppose
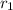 and
and
 are the roots of the equation
are the roots of the equation
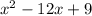 to find
to find
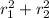 , note that from our Vieta's formula for quadratics we have
, note that from our Vieta's formula for quadratics we have
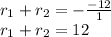 and
and
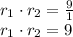
Therefore