Question

Because all airline passengers do not show up for their reserved seat, an airline sells 125 tickets for a flight that holds only 120 passengers. The probability that a passenger does not show up is 0.10, and the passengers behave independently. a. What is the probability that every passenger who shows up can take the flight? b. What is the probability that the flight departs with empty seats?

Answer 1

a) 0.9961

b) 0.9886

Explanation:

If X is the variable define by people who do not show up to take their flight, and considering that the probability of success (the person shows up) is 0.90, and the probability of fail (the person doesn't show up) is 0.10, the variable X has a binomial distribution.

The binomial distribution formula would be:

×
`P(X=k) = C_(x|k) 0.1^(k)`×
`0.9^(125-k)`

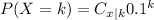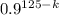
a) What is the probability that every passenger who shows up can take the flight?

This happens when X≥5

P( X≥5) = 1 - (P(X=0) + P(X=1) + P(X=2) + P(X=3) + P(X=4)) = 0.9961

a) What is the probability that the flight departs with empty seats?

This happens when X>5

P(X>5) = 1 - P(X≤5) = 1 - (P(X=0) + P(X=2) + P(X=3) + P(X=4) + P(X=5)) = 0.9886