Question

A company that manufactures large LCD screens knows that not all pixels on their screen​ light, even if they spend great care when making them. They know that the manufacturing process has a blank pixel​ rate, on​ average, of 4.4 blank pixels in a sheet 4 ft by 8 ft that will be cut into smaller screens. They believe that the occurrences of blank pixels are independent. Their warranty policy states that they will replace any screen sold that shows more than 2 blank pixels. Suppose the number of blank pixels can be modeled by a Poisson distribution. Complete parts​ a) through​ d) below. a) What is the mean number of blank pixels per square foot? The mean is pixel(s). b) What is the standard deviation of blank pixels per square foot? The standard deviation is pixel(s). c) What is the probability that a 2 ft by 3 ft screen will have at least one defect? A 2 ft by 3 ft screen will have at least one defect with probability. d) What is the probability that a 2 ft by 3ft screen will be replaced because it has too many defects? A 2 ft by 3 ft screen will need to be replaced with probability .

Answer 1

a) 0.1375

b) 0.3708

c) 0.56

d) 0.05

Explanation:

a) If 4.4 is the mean number of blank in a sheet 4ft x 8 ft = 32ft^2. Then the mean number of blank per square foot is 4.4/32 =0.1375

b) X=Number of blank pixels per ft^2

`X=Poisson(\lambda), E[X]=\lambda=0.1375, Var(X)=\lambda, \sigma =√(\lambda) =√(0.1375)=0.3708`

c) The mean number of blank in a sheet 2ft x 3 ft = 6ft^2 is 6*0.1375=0.825

Then
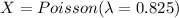
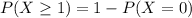
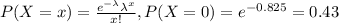
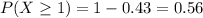
`X=Poisson(\lambda=0.825)`

`P(X\geq 1)=1-P(X=0)`

`P(X=x)=(e^(-\lambda)\lambda^x)/(x!), P(X=0)=e^(-0.825)=0.43`

`P(X\geq 1)=1-0.43=0.56`

d)
`P(X>2)=1-P(X\leq 2)=1-\sum_(i=0)^(2)P(X=i)`

`P(X>2)=1-\sum_(i=0)^(2)(e^(-\lambda)\lambda^(i))/(i!), \lambda=0.825`

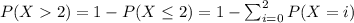
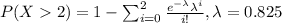
P(X>2)=1-0.94=0.05