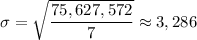Answer:
See explanation
Explanation:
Arrange the salaries $41,027, $35,901, $31,159, $33,664, $35,166, $39,338, $32,691 in ascending order:
$31,159, $32,691, $33,664, $35,166, $35,901, $39,338, $41,027
A) The mean salary (to the nearest dollar) is
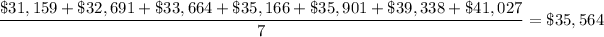
B) Minimum


Median
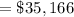
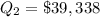
Maximum
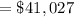
C) The standard deviation of this data set can be calculated using formula
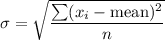
First, find
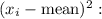
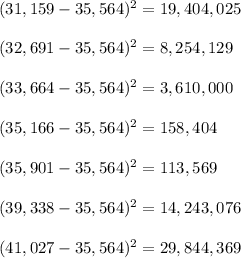
Now,