Question

Formulate a system of equations for the situation below and solve. Michael Perez deposited a total of $2000 with two savings institutions. Bank A pays interest at the rate of 6%/year, whereas Bank B pays interest at the rate of 8%/year. If Michael earned a total of $144 in interest during a single year, how much did he deposit in each institution? Bank A $ Bank B $

Answer 1

Amount deposited in Bank A = $800

Amount deposited in Bank B = $1200

Explanation:

In the question,

Total amount deposited by Michael Perez in the Banks A and B = $2000

Interest rate of Bank A = 6% / year

Interest rate of Bank B = 8% / year

Also,

Total Interest earned by both the banks in a year = $144

Now,

Let us say the amount deposited in Bank A is = x

and,

Amount deposited in Bank B = (2000 - x)

So,

`(6)/(100)x+(8)/(100)(2000-x)=144\\0.06x+0.08(2000)-0.08x=144\\-0.02x+160=144\\0.02x=16\\x=800`

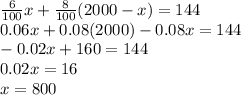
Therefore,

Amount deposited in Bank A = $800

and,

Amount deposited in Bank B = $1200

Answer 2

DA= $800 and DB= $1200

Explanation:

Equation I (Interest of Bank A):

IA= 0.06/year*DA *1year (DA= Deposit in Bank A)

IA= 0.06*DA

Equation II (Interest of Bank B):

IB= 0.08/year*DB *1year (DB= Deposit in Bank B)

IB= 0.08*DB

Total interest:

TI=IA+IB=$144

Total deposit:

TD= DA +DB= $2000

Adding equations I and II:

IA+IB = 0.06DA +0.08DB

$144= 0.06DA+0.08DB

(DB= $2000-DA)

When replacing DB:

$144= 0.06DA + 0.08($2000-DA)

Applying distributive property:

$144= 0.06DA + (0.08*$2000) -0.08DA

$144= -0.02DA + $160

0.02DA= $160-$144

0.02DA = $16

DA= $16/0.02

DA= $800

DB= $2000-$800

DB= $1200