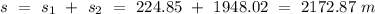Question

A model rocket blasts off from the ground, rising straight upward with a constant acceleration that has a magnitude of 85.0 m/s2 for 2.30 seconds, at which point its fuel abruptly runs out. Air resistance has no effect on its flight. What maximum altitude (above the ground) will the rocket reach?

Answer 1

Maximum height attained by the model rocket is 2172.87 m

Step-by-step explanation:

Given,

• Initial speed of the model rocket = u = 0
• acceleration of the model rocket =
  `a\ =\ 85.0 m/s^2`
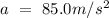
• time during the acceleration = t = 2.30 s

We have to consider the whole motion into two parts

In first part the rocket is moving with an acceleration of a = 85.0
`m/s^2` for the time t = 2.30 s before the fuel abruptly runs out.

Let
`s_1` be the height attained by the rocket during this time intervel,

`s_1\ =\ ut\ +\ (1)/(2)at^2\\\Rightarrow s_1\ =\ 0\ +\ 0.5* 85* 2.30^2\\\Rightarrow s_1\ =\ 224.825\ m`

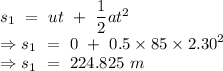
And Final velocity at that point be v

`\therefore v\ =\ u\ +\ at\\\Rightarrow v\ =\ 0\ +\ 85.0* 2.3\\\Rightarrow v\ =\ 195.5\ m/s.`

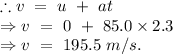
Now, in second part, after reaching the altitude of 224.825 m the fuel abruptly runs out. Therefore rocket is moving upward under the effect of gravitational acceleration,

Let '
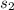`s_2`' be the altitude attained by the rocket to reach at the maximum point after the rocket's fuel runs out,

At that insitant,

• initial velocity of the rocket = v = 195.5 m/s.

• a =
  `-g\ =\ -9.81\ m/s^2`
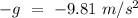
• Final velocity of the rocket at the maximum altitude =
  `v_f\ =\ 0`

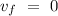
From the kinematics,

`v^2\ =\ u^2\ +\ 2as\\\Rightarrow 0\ =\ u^2\ -\ 2gs_2\\\Rightarrow s_2\ =\ (u^2)/(2g)\\\Rightarrow s_2\ =\ (195.5^2)/(2* 9.81)\\\Rightarrow s_2\ =\ 1948.02\ m`

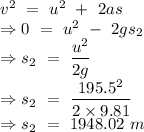
Hence the maximum altitude attained by the rocket from the ground is

`s\ =\ s_1\ +\ s_2\ =\ 224.85\ +\ 1948.02\ =\ 2172.87\ m`