Answer:
a) 2.5%
b) 97.5%
c) 16%
d) 84%
e) 50%
f) 50%
g) 84%
h) 16%
i) 97.5%
j) 2.5%
Explanation:
The empirical rule, or the rule of 50%-34%-14%, states that:
In a normally distributed stat with mean
 and standard deviation
and standard deviation
 ...
...
a) 2.5% of the scores are going to be above
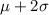
b) 13.5% of the scores are going to be above
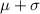 and below
and below
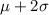 .
.
c) 34% of the scores are going to be above
 and below
and below
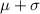
d) 34% of the scores are going to be above
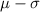 and below
and below

e) 13.5% of the scores are going to be above
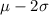 and below
and below
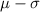
f) 2.5% of the scores are going to be below
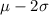
In this problem
We have that
 and
and
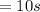
So:
(a) above 100, (b) below 100

So 2.5% of the scores are going to be above 100, and the other 97.5% is going to be below 100
c) above 90, (d) below 90
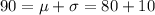
So 13.5% of the scores are going to be above 90 and below 100, and 2.5% of the scores are going to be above 100. So 13.5% + 2.5% = 16% of the scores are going to be above 90 and the other 84% is going to be below 90
(e) above 80, (f) below 80
80 is the mean, so approximately 50% percent of the scores are going to be above 80 and 50% are going to be below 70%.
(g) above 70, (h) below 70
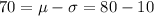
34% of the scores are going to be above 70 and below 80, and other 50% percent of the scores are going to be above 80. So in all, 84% of the scores are going to be above 70. The other 16% of the scores are going to be below 70.
(i) above 60, and (j) below 60
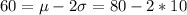
So 2.5% of the scores are going to be below 60, and the other 97.5% is going to be above 100