Answer:
The value of k is 6
Explanation:
we know that
If two segments are parallel, then their slopes are the same
we know that
The formula to calculate the slope between two points is equal to
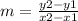
step 1
Find the slope MN
we have
M(0, −3), N(−2, −4)
substitute
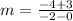
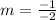
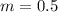
step 2
Find the slope AB
A(2, 5), B(4, k)
substitute in the formula
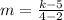
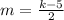
Remember that the slopes MN and AB must be equal
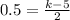
Solve for k
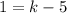
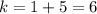
therefore
The value of k is 6