Question

Show that ∆ABC is a right triangle if A(0, 0), B(3, 2), and C(–2, 3). Find the slope m1 of AB and the slope m2 of AC and verify that m1m2 = –1. Provide your complete solutions and proofs.

Answer 1

First we'll show this is a right triangle by the Pythagorean Theorem:

`A(0,0), B(3,2), C(-2, 3)`

`AB^2=3^2+2^2=13`

`AC^2=(-2)^2+3^2=13`

`BC^2 = (-3 -3)^2 + (3 -2)^2 = 26`

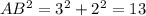
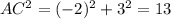
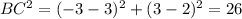
Since
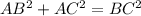`AB^2+AC^2=BC^2` we have a right triangle, by the (converse to the) Pythagorean Theorem. We also see it's isosceles, AB=AC.

`\textrm{Slope of AB} = m_1 = (2 - 0)/(3 - 0) = \frac 2 3`

`\textrm{Slope of AC} = m_2 = (3 - 0)/(-2 - 0) = -\frac 3 2`

`m_1 m_2 = (\frac 2 3)(-\frac 3 2 ) = -1 \quad\checkmark`

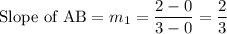
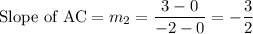
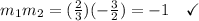
That's the end of the homework but I'll go on a bit.

Another way to show perpendicularity, essentially the same as the other two, is by a zero as the dot product of the sides as vectors, differences between vertices.

Vector AB = B - A = (3,2)

Vector AC = C - A = (-2, 3)

AB · AC = 3(-2) + 2(3) = 0

A zero dot product means

AB ⊥ AC