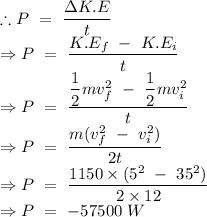Question

Determine the power required for a 1150kg car to climb a 100-m-long uphill road with a slope of 30° (from horizontal) in 12s (a) at a constant velocity, (b) from rest to a final velocity of 30 m/s, and (c) from 35 m/s to a final velocity of 5 m/s. Disregard friction, air drag, and rolling resistance.

Answer 1

part (a) 46958.33 W

part (b) 43125 W

part (c) -57500 W

Step-by-step explanation:

Given,

• Mass of the car = m = 1150 kg
• Angle of inclination of the hill =
  `\theta\ =\ 30^o`
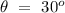
• Total time taken = t = 12 s

part (a)

Given that the velocity is constant,

Total displacement traveled by the car = s = 100 m

Work done by the car to reach at the top of the hill

`w\ =\ mgsin30^0* s\\\Rightarrow w\ =\ 1150* 9.81* sin30^o* 100\\\Rightarrow w\ =\ 563500\ J`

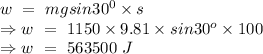
Hence, power
`P \ =\ (w)/(t)\\\Rightarrow P\ =\ (563500)/(12)\\\Rightarrow P\ =\ 46958.33\ W`

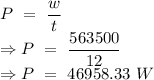
part (b)

Given,

• final velocity =
  `v_f\ =\ 30\ m/s.`
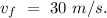
• Initial velocity =
  `v_i\ =\ 0\ m/s`

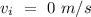
Total power is equal to the ratio of the change in kinetic energy and total time taken

`\therefore P\ =\ (\Delta K.E)/(t)\\\Rightarrow P\ =\ (K.E_f\ -\ K.E_i)/(t)\\\Rightarrow P\ =\ ((1)/(2)mv_f^2\ -\ 0)/(t)\\\Rightarrow P\ =\ (mv_f^2)/(2t)\\\Rightarrow P\ =\ (1150* 30^2)/(2* 12)\\\Rightarrow P\ =\ 43125\ W`

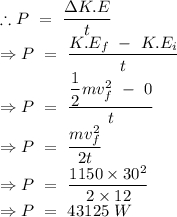
part (c)

• Initial velocity of the car =
  `v_i\ =\ 35\ m/s.`
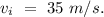
• Final velocity of the car =
  `v_f\ =\ 5 m/s.`

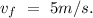
Total power is equal to the ratio of the change in kinetic energy and total time taken

`\therefore P\ =\ (\Delta K.E)/(t)\\\Rightarrow P\ =\ (K.E_f\ -\ K.E_i)/(t)\\\Rightarrow P\ =\ ((1)/(2)mv_f^2\ -\ (1)/(2)mv_i^2)/(t)\\\Rightarrow P\ =\ (m(v_f^2\ -\ v_i^2))/(2t)\\\Rightarrow P\ =\ (1150* (5^2\ -\ 35^2))/(2* 12)\\\Rightarrow P\ =\ -57500\ W`