Question

an automated filling operation, the probability of an incorrect fill when the process is operated at a low speed is 0.001. When the process is operated at a high speed, the probability of an incorrect fill is 0.01. Assume that 20% of the containers are filled when the process is operated at a high speed and the remainder are filled when the process is operated at a low speed. Round your answers to four decimal places (e.g. 98.7654). (a) What is the probability of an incorrectly filled container? (b) If an incorrectly filled container is found, what is the probability that it was filled during the high-speed operation?

Answer 1

(a) 0.0028 (b) 0.7143

Explanation:

First of all, let's define the following events:

I: a container is filled incorrectly

L: a process is operated at a low speed

H: a process is operated at a high speed

S: the sample space

Then, we have according to the original text that

P(I | L) = 0.001, P(I | H) = 0.01, P(H) = 0.2, P(L) = 0.8

and we are seeking the following probabilities (a) P(I) and (b) P(H | I)

(a) P(I) = P(I∩S) = P[I∩(L∪H)] (because L∪H=S)

= P[(I∩L)∪(I∩H)] (distributive laws)

= P(I∩L)+P(I∩H) (because L and H are mutually exclusive)

= P(I | L)P(L)+P(I | H)P(H)

= (0.001)(0.8)+(0.01)(0.2) = 0.0028

On the other hand,

(b) P(H | I) =
`(P(I\cap H))/(P(I))`

=
`(P(I | H)P(H))/(P(I))`

=
`((0.01)(0.2))/(0.0028)`

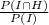
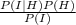
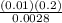
= 0.7143