Question

Niemann–Pick disease is a fatal lysosomal storage metabolic disorder caused by an autosomal recessive allele. A couple, both of whom are heterozygous for the allele, are wanting to start a family. They are hoping to have three children. What is the probability that if they have three children, none of them will have Niemann–Pick disease?A. 1/4`B. 1/3C. 2/3D. 9/64E. 27/64

Answer 1

E. 27/64

Step-by-step explanation:

Knowing that the couple is heterozygous (Aa) for Niemann-Pick disease, they can have children with the following pairs of alleles:

A x A = AA (Dominant homozygous - Unaffected)

A x a = Aa (Heterozygous - Unaffected)

a x A = Aa (Heterozygous - Unaffected)

a x a = aa (Recessive homozygous - Affected)

So each allele pair has a probability of:

AA = 1/4

Aa = 1/4

Aa = 1/4

aa = 1/4

As the disease only affects recessive homozygous individuals (aa), the probability of an unaffected child being born is 3/4.

Since the couple expects to have three children, the probability of neither being born with the disease is obtained by multiplying the probability of each, as follows:

`3/4 * 3/4 * 3/4 = 27/64`

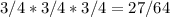
Thus, it is concluded that the probability of none of the children having Niemann-Pick syndrome is 27/64.