Question

A jogger runs 140 m due west, then changes direction for the second leg of her run. At the end of the run, she is 374 m away from the starting point at an angle of 20o north of west. What were the length and direction of her second displacement?

Answer 1

The length of her second displacement = 247.12 m.

The direction of her second displacement = 31.24° from west.

Explanation:

As per the question,

From the figure as drawn below,

Let the starting point be O. After running 140 m due west, she reached at point A.

∴ OA = 140 m

And At the end of the run, she is 374 m away from the starting point at an angle of 20° north of west.

∴ OP = 374 m

We have to find the distance AP = x.

By using the cosine rule in triangle OAP

`cos \theta = (OA^(2)+OP^(2)-AP^(2))/(2* OA* OP)`

After putting the given value, we get

`cos 20= (140^(2)+374^(2)-x^(2))/(2* 140* 374)`

`x^(2)=140^(2)+374^(2) - 2* 140* 374* cos 20`

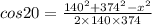
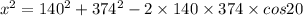
∴ x = 247.12 m

Hence,the length of her second displacement = 247.12 m.

Again,

By using the cosine rule in triangle OAP, we get

`cos \alpha = (OA^(2)+AP^(2)-OP^(2))/(2* OA* AP)`

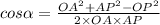
After putting the given value, we get

`cos \alpha = (140^(2)+247.12^(2)-374^(2))/(2* 140* 247.12)`

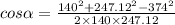
∴ α = 148.759°

Hence, the direction of her second displacement = 180° - α = 180° - 148.759 = 31.24° from west.