Question

Given the following balanced equation at 120°C: A(g) + B(g) ⇋ 2 C(g) + D(s)(a) At equilibrium a 4.0 liter container was found to contain 1.60 moles of A, and 0.40 moles of B, and 0.40 moles of C, and 1.60 moles of D. Calculate Kc.(b) If 0.20 moles of B and 0.20 mole of C are added to this system, what will be the new equilibrium concentration of A be?(c) If the volume of the container in which the system is at equilibrium [part (a)] is suddenly halved, what will be the new equilibrium concentrations?

Answer 1

a) Kc = 0.1

b) Kc = 0.15

c) The concentrations are:

[A] = 0.8 mol/L

[B] = 0.2 mol/L

[C] = 0.2 mol/L

[D] = 0.8 mol/L

Step-by-step explanation:

The reaction is:

A + B ⇄ 2C + D

a) The Kc is equal:

`K_(c) =([C]^(2)[D] )/([A][B]) =((n_(C)/V)^(2)(n_(D)/V) )/((n_(A)/V)((n_(B)/V) ) =(n_(c)^(2) (n_(D)/V))/(n_(A)n_(B) )`

Where

nA = 1.6

nB = 0.4

nC = 0.4

nD = 1.6

V = 4 L

Replacing

`K_(c) =(0.4^(2)*(1.6/4) )/(1.6*0.4) =0.1`

b) When 0.2 moles is added

nC = 0.4 + 0.2 = 0.6

nB = 0.4 + 0.2 = 0.6

`K_(c) =(0.6^(2)*(1.6/4) )/(1.6*0.6) =0.15`

c) If the volume is halved:

V = 4/2 = 2 L

The new equilibrium concentrations are:

`[A]=(n_(A) )/(V) =(1.6)/(2) =0.8 mol/L`

`[B]=(n_(B) )/(V) =(0.4)/(2) =0.2 mol/L\\`

`[C]=(n_(C) )/(V) =(0.4)/(2) =0.2 mol/L`

`[D]=(n_(D) )/(V) =(1.6)/(2) =0.8 mol/L`

Answer 2

a) kc = 0,25

b) [A] = 0,41 M

c) [A] = 0,8 M

[B] =0,2 M

[C] = 0,2M

Step-by-step explanation:

The equilibrium-constant expression is defined as the ratio of the concentration of products over concentration of reactants. Each concentration is raised to the power of their coefficient.

Also, pure solid and liquids are not included in the equilibrium-constant expression because they don't affect the concentration of chemicals in the equilibrium.

If global reaction is:

A(g) + B(g) ⇋ 2 C(g) + D(s)

The kc =
`([C]^2)/([A][B])`

a) The concentrations of each compound are:

[A] =
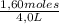`(1,60 moles)/(4,0 L)` = 0,4 M

[B] =
`(0,40 moles)/(4,0 L)` = 0,1 M

[C] =
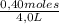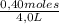`(0,40 moles)/(4,0 L)` = 0,1 M

kc =
`([0,1]^2)/([0,4][0,1])` = 0,25

b) The addition of B and D in the same amount will, in equilibrium, produce these changes:

[A] =
`(1,60-x moles)/(4,0 L)`

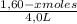
[B] =
`(0,60-x moles)/(4,0 L)`

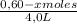
[C] =
`(0,60+2x moles)/(4,0 L)`

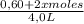
0,25 =
`([0,60+2x]^2)/([1,60-x][0,60-x])`

You will obtain

3,75x² +2,95x +0,12 = 0

Solving

x =-0,74363479081119 → No physical sense

x =-0,043031875855476

Thus, concentration of A is:

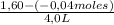`(1,60-(-0,04 moles))/(4,0 L)` = 0,41 M

c) When volume is suddenly halved concentrations will be the concentrations in equilibrium over 2L:

[A] =
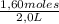`(1,60 moles)/(2,0 L)` = 0,8 M

[B] =
`(0,40 moles)/(2,0 L)` = 0,2 M

[C] =
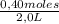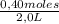`(0,40 moles)/(2,0 L)` = 0,2M

I hope it helps!